Stochastic Process

§1 Introduction

§§1.2 Kolmogorov Thm. and Separability

1. Kolmogorov Theorem

Proposition: Suppose is a Polish space with a compatible probability measure family , then there is a probability on s.t. coincides with on finite rectangle parabolic set on .

2. Separability

Definition: Separability of stochastic process: open interval , closed set , ,
, a.e
If is separable, then , a.e. -measurable. (), when

3. Shift Operator

Definition: (Shift operator) Let , is closed under addition. Define s.t. . Then is measurable. From we get a set operator : , . And a function operator : . If , then .

§§1.3 Independent Increment Process and Martingale

1. Independent Increment Process

Definition: Independent increment process: , are independent

Properties:

• Suppose , . Then , .
• and -measurable function . . (Markov property)
  Proof:
  lemma: Let be a probability space, is a sub--field of , and are measurable spaces, is a -valued r.v. , is a -valued r.v. . Suppose is independent of . Let be a -measurable function on s.t. , then .
  It’s sufficient to show that is -measurable which follows from the lemma noticing that .*

2. Martingale

Martingale: is a martingale, if , , . Especially, when , we call is a martingale for short.

Proposition: is a martingale, then $\mathbb{E}(\xi_t|\mathscr{F}_s) = \xi_s, \forall s \leq t \iff \mathbb{E}(\xi_{t_{n + 1}} | \xi_{t_0}, \dots, \xi_{t_n}) = \xi_{t_n}, \forall t_1 < t_2 < \dots < t_n \in T.$
Proof:
: .
: It’s sufficient to show that , which follows from the left side directly.*

Remark: All real-valued independent increment processes with constant mean are martingale but the opposite is not true. Because , when is a process with independent increment and constant mean, the first term of the rhs equals , but this doesn’t necessarily mean is in independent with .

3. Properties of Process with Independent Increment and Stable Process

Definition: ==Stable Process==: s. t. .
Example: Brown motion ,

§§1.4 Markov Process

Definition: ==Markov Process== Suppose is a stochastic process on and takes values on , is a family of -algebra s.t. , , is adapted w.r.t. . We call is a Markov process when , . Especially, when , we call is the Markov process on .

Proposition: is a Markov process on , iff , , .

Proof: : Trivial.

: We only need to show that , . Let . We can see that , , so the family of finite dimensional rectangle parabolic sets . And it’s easy to check that is a -system, thus .

Proposition: The followings are equivalent.

1. is a Markov process
2. and bounded real-valued function , $\mathbb{E}(f(\xi_t) | \mathscr{F}_s) = \mathbb{E}(f(\xi_t) | \xi_s).$
3. Let , bounded real-valued r.v , .
4. bounded real-valued function and , , .

Proof: 2 3: For measurable real-valued function and ,

$$\begin{align} \mathbb E(f_1(\xi_{t_1})f_2(\xi_{t_2}) | \mathscr F_s) &= \mathbb E(f_1(\xi_{t_1})\mathbb E(f_2(\xi_{t_2}) | \mathscr F_{t_1}) | \mathscr F_s)\\ &=\mathbb E(f_1(\xi_{t_1})\mathbb E(f_2(\xi_{t_2}) | \xi_{t_1}) | \mathscr{F}_{s}))\\ &=\mathbb E(f_1(\xi_{t_1})\mathbb E(f_2(\xi_{t_2}) | \mathscr \xi_{t_1}) | \xi_s))\\ &= \mathbb E(f_1(\xi_{t_1}) \mathbb E(f_2(\xi_{t_2}) | \mathscr{F}_{t_1}) | \xi_s)\\ &= \mathbb E(\mathbb E(f_1(\xi_{t_1})f_2(\xi_{t_2}) | \mathscr{F}_{t_1}) | \xi_{s})\\ &= \mathbb E(f_1(\xi_{t_1}) f_2(\xi_{t_2}) | \xi_s) \end{align}$$

By reduction, and ,

$$\mathbb E(f_1(\xi_{t_1})f_2(\xi_{t_2})\cdots f_n(\xi_{t_n}) | \mathscr F_s)\\ =\mathbb E(f_1(\xi_{t_1})f_2(\xi_{t_2})\cdots f_n(\xi_{t_n}) | \xi_s).$$

Especially, ,

$$\mathbb E(\chi_{A_1}(\xi_{t_1})\cdots \chi_{A_n}(\xi_{t_n}) | \mathscr F_s) = \mathbb E(\chi_{A_1}(\xi_{t_1}) \cdots \chi_{A_n}(\xi_{t_n}) | \xi_s).$$

Let

$$\begin{align} \mathscr S \triangleq& \{B | B = \{\omega ; \xi_{t_1} \in A_1, \cdots, \xi_{t_n} \in A_n\},\\ &\text{ for some } t_n > t_{n-1} > \cdots > t_1 \geq s; A_1, \dots, A_n \in \Sigma, n \geq 1\}\\ \mathscr H \triangleq& \{g \in \mathscr F^t | \mathbb E(g | \mathscr F_s) = \mathbb E (g | \xi_s) \}. \end{align}.$$

Obviously, is a system. And , , and . Hence by monotone class thm. of function. All measurable function belong to .

Remark: ’s conditional expectation w.r.t. ’s given value and the initial distribution determine the distribution of .

Definition: , .

---

Theorem:

Definition: (family of transitive probability):

1. For fixed , is a probability measure on ;
2. For fixed , is a - measurable function.
3. , we have Kolmogorov-Chapman equation: $$p(s, x; t, A) = \int p(s, x; r, \mathrm{d}y) p(r, y; t, A)$$

Proposition: Let is a complete divisible metric space generated measure space; is a transitive probability measure family, then we can construct a measure space and a Markov process , s.t.

$$\mathbb P([\xi_t \in A]) = p(s, x; t, A).$$

Proof: We use Kolmogorov theorem to construct probability space. For this, let , is the family of finite dimension measurable sets on , . For and . Let

$$F_{t_1, \dots, t_n}(\tilde A) = \int p_0(\mathrm{d} x_0) \int p(0, x_0; t_1, \mathrm d x_1) \cdots \int p(t_{n - 1}, x_{n - 1}; t_n, \mathrm d x_n) \chi_{\tilde A}.$$

Theorem(Tulcea):

• ;
• compactness, $A_n(\omega) \triangleq \bigcap_{A \in \mathscr F_n, \omega \in A} A.$for any sequence , .
  , , , satisfy that is a measure on , is a probability measure on for given and for given , is -measurable. 1. and 2. hold. Then probability measure on s.t.

• (i.e. );
• $$\begin{align} \mathbb E(\chi_A | \mathscr F_{n - 1}) = Q_n(\omega; A)(\forall A \in \mathscr F_n) \\ \iff \int_{A \cap B} \mathrm d \mathbb P = \int_B Q_n(\omega; A) \mathbb P(\mathrm d \omega) (\forall A \in \mathscr F_n, B \in \mathscr F_{n - 1}) \\ \implies \mathbb P(A) = \int Q_n(\omega; A) \mathbb P(\mathrm d \omega) (\forall A \in \mathscr F_n). \end{align}$$

  §§1.5 Gauss System

Definition(Gauss system): We a stochastic process on is a Gauss system if for ’s joint distribution is Gaussian, i.e.

$$\mathbb E \exp^{\imath \sum_{k = 1}^{n} \lambda_k \xi_{t_k}} = \exp^{\imath \sum_{k = 1}^n \lambda_k \mathbb E(\xi_{t_k}) - \frac{1}{2}\sum_{i,j}\lambda_i \mathrm{Cov}(\xi_{t_i},\xi_{t_j})\lambda_j}$$

Proposition: is a Gauss system iff any finite r.v.’s linear combination is a -dimension Gaussian distribution, i.e. , is real number, r.v. .

Proposition: For

Proposition: Let is a Gauss system, then:

1. is independent iff .
2. is independent with iff .

Proposition: Let is a Gauss system, and let , then . Then . And is Gaussian.
Proof: , . And .

§§2.2 Stopping Time and Stopping Theorem of Martingale

§§2.4 Stopping Theorem(General)

Theorem: Let

Markov Chain

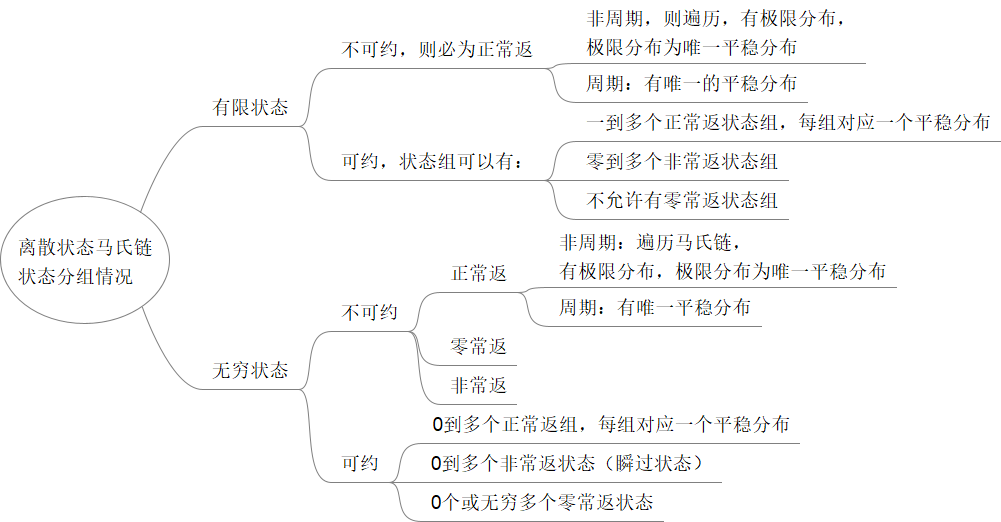
Suppose is a dimension Brown motion. Prove that is a martingale.